Selection Sort

选择排序,即依次在待排序列表中找出最小者,放置到待排序列表最左端。初始时,待排序列表为整个列表。
def selection_sort(lst):
def _min(start):
value = lst[start]
index = start
for i in range(start + 1, len(lst)):
if lst[i] < value:
value = lst[i]
index = i
return index
for i in range(len(lst) - 1):
min_index = _min(i)2211
if min_index != i:
lst[i], lst[min_index] = lst[min_index], lst[i]
return lst
时间复杂度,O(n2)
Insertion Sort
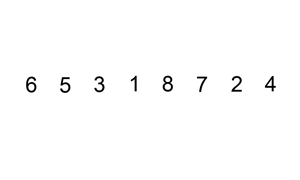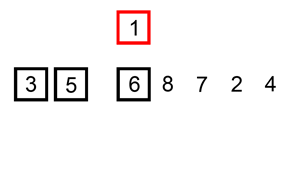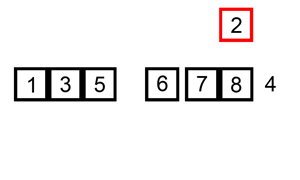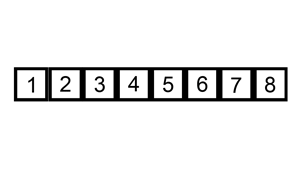
插入排序,意为将新元素插入到已排序元素中的合适位置。初始时,已排序元素为第一个元素,然后从第二个元素开始将其依次插入到合适位置。插入时,从右往左依次与已排序元素进行比较,若待插入元素比已排序元素小,则将已排序元素向后移动一位,直到找到合适位置。
def insertion_sort(lst):
for i in range(1, len(lst)):
ptr = i - 1
temp = lst[i]
while ptr >= 0 and temp < lst[ptr]:
lst[ptr + 1] = lst[ptr]
ptr -= 1
lst[ptr + 1] = temp
return lst
最好情况,列表已从小到大排序,时间复杂度O(n);最坏情况,列表已从大到小排序,时间复杂度O(n2)
Shell Sort
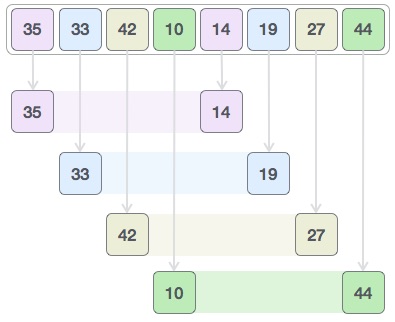
作为插入排序的改进版,希尔排序通过将列表分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序,算法的最后一步就是普通的插入排序,但是到了这步,需排序的数据几乎是已排好的了(此时插入排序较快)。
假设有一个很小的数据在一个已按升序排好序的数组的末端。如果用复杂度为O(n2)的排序(冒泡排序或插入排序),可能会进行n次的比较和交换才能将该数据移至正确位置。而希尔排序会用较大的步长移动数据,所以小数据只需进行少数比较和交换即可到正确位置。
每次排序的分区大小由步长值gap决定,有多种步长值可供选择。下面选择length/2k
def shell_sort(lst):
gap = len(lst) // 2
while gap >= 1:
for start in range(gap):
for i in range(start, len(lst), gap):
# insertion
ptr = i - gap
temp = lst[i]
while ptr >= 0 and temp < lst[ptr]:
lst[ptr + gap] = lst[ptr]
ptr -= gap
lst[ptr + gap] = temp
gap //= 2
return lst
时间复杂度根据gap序列而定。
Bubble Sort
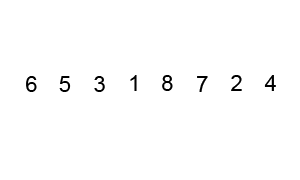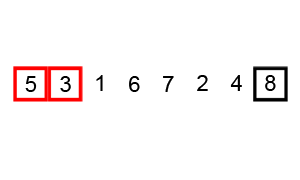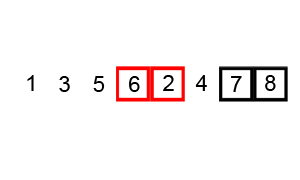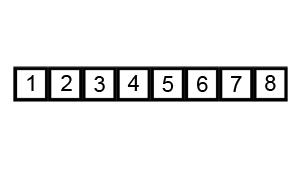
冒泡排序,即不断地通过相邻两元素交换,将较大或较小者交换到列表一端。若在某趟排序中,并没有发生元素交换,则说明所有元素已经排序完成。
def bubble_sort(lst):
for end in range(len(lst) - 1, 0, -1):
swapped = False
for i in range(end):
if lst[i] > lst[i + 1]:
lst[i], lst[i + 1] = lst[i + 1], lst[i]
swapped = True
if not swapped:
break
return lst
最好情况,列表已从小到大排序,时间复杂度O(n);最坏情况,要进行n-1次遍历交换操作,时间复杂度O(n2)
Quick Sort
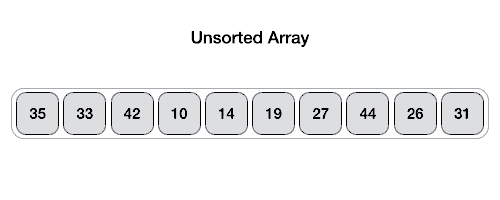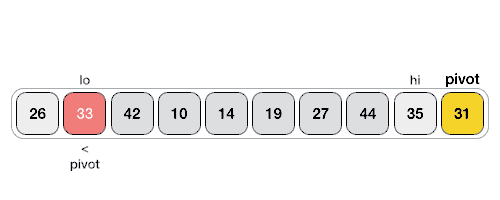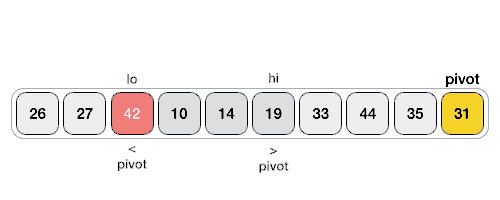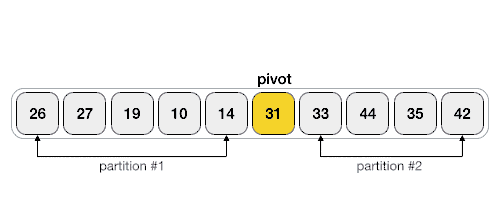
快速排序,即从列表中选一个元素作为中心点,将其余元素中小于该值者归为一类,大于或等于该值者归为一类,然后分别对上述两类元素集进行快速排序。
def quick_sort(lst):
def sort(left, right):
if left < right:
p_left = left
p_right = right + 1
while p_left < p_right:
p_left += 1
p_right -= 1
while p_left <= right and lst[p_left] < lst[left]:
p_left += 1
while p_right >= left and lst[p_right] > lst[left]:
p_right -= 1
if p_left < p_right:
lst[p_left], lst[p_right] = lst[p_right], lst[p_left]
lst[left], lst[p_right] = lst[p_right], lst[left]
sort(left, p_right - 1)
sort(p_right + 1, right)
sort(0, len(lst) - 1)
return lst
最坏情况下,列表已排序,时间复杂度O(n2);平均情况,时间复杂度O(nlog2n)
Merge Sort
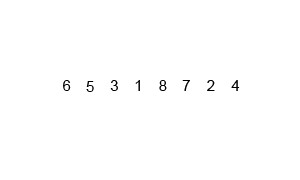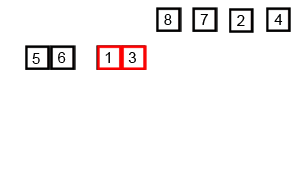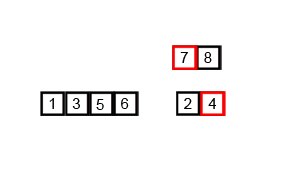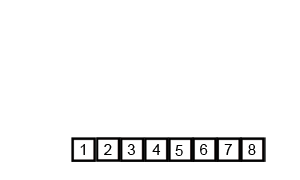
归并排序,将有n个元素的列表视为由n个子列表组成,然后两两合并子列表,排序之,然后继续合并合并后的子列表,直到合并成一个列表。
def merge_sort(lst):
last = len(lst) - 1
def merge(left, right, count):
temp = []
end = right + count - 1 if right + count - 1 <= last else last
p_left = left
p_right = right
while p_left < right and p_right <= end:
if lst[p_left] <= lst[p_right]:
temp.append(lst[p_left])
p_left += 1
else:
temp.append(lst[p_right])
p_right += 1
if p_left <= right - 1:
temp += lst[p_left:right]
if p_right <= end:
temp += lst[p_right: end + 1]
for i in range(len(temp)):
lst[left + i] = temp[i]
count = 1
while count < len(lst):
left = 0
right = count
while right <= last:
merge(left, right, count)
left += count * 2
right += count * 2
count *= 2
return lst
count的取值不超过[O(log2n)],因此最多合并O(log2n)次,每次合并都要遍历所有n元素,故时间复杂度为O(nlog2n)
Heap Sort

堆有以下性质:
- 任意节点小于(或大于)它的所有后裔,最小元(或最大元)在堆的根上(堆序性)。
- 堆总是一棵完全树。即除了最底层,其他层的节点都被元素填满,且最底层尽可能地从左到右填入。
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆排序使用二叉堆,二叉堆可以用一维数组表示:
- 父节点i的左子节点在位置(2*i+1);
- 父节点i的右子节点在位置(2*i+2);
- 子节点i的父节点在位置floor((i-1)/2);
堆排序算法如下:
- 构建最大堆(先将初始序列视为完全二叉树,然后将其调整为最大堆)
- 将堆顶元素与堆底最右元素交换,相当于取出最大者。并将堆底最后元素从堆中移除
- 交换后,当前二叉树可能不满足堆的性质。因此,将堆顶元素下移,找到其合适位置,使之再次满足堆的性质
- 不断地交换堆底与堆顶元素,直至堆中只剩下一个元素
def heap_sort(lst):
def heapify():
for start in range(((len(lst) - 1) // 2), -1, -1):
shift_down(start, len(lst) - 1)
def shift_down(start, end):
if start * 2 + 1 > end:
return
left_index = start * 2 + 1
right_index = start * 2 + 2
parent = lst[start]
left = lst[left_index]
right = lst[right_index] if right_index <= end else left - 1
if parent < max(left, right):
if left > right:
lst[start], lst[left_index] = lst[left_index], lst[start]
shift_down(left_index, end)
else:
lst[start], lst[right_index] = lst[right_index], lst[start]
shift_down(right_index, end)
heapify()
for end in range(len(lst) - 1, 0, -1):
lst[0], lst[end] = lst[end], lst[0]
shift_down(0, end - 1)
return lst
shift_down执行时间不超过O(log2n),故时间复杂度为O(nlog2n)
稳定性分析
稳定性指的是,对列表中任意相同的两个元素,排序后,二者的相对次序不变。
- Selection Sort: 不稳定。选择最小元素后会将其交换到未排序区首端,此时可能破坏相对次序
- Insertion Sort: 稳定。依次插入时不会破坏相对次序
- Shell Sort: 不稳定。 会将相同元素分到不同组,排序后打乱相对次序。
- Bubble Sort: 稳定。交换过程中遇到相同元素不会交换
- Quick Sort: 不稳定。交换元素时可能破坏稳定性
- Merge Sort: 稳定。合并子序列时,若左右两侧元素相等,会优先选择左侧元素
- Heap Sort: 不稳定。堆顶元素与堆底元素交换时可能会破坏稳定性
为啥要稳定呢?因为当分别对元素的某个关键字进行排序时,就不能随便打乱相对次序了。比如对人名排序(“姓+名”),“Smith Bob”、“Smith Jone”先按last name排,再按first name排。
源码见https://gist.github.com/YieldNull/cbe70dc07f0c53c73b2478ec6b877882